Dehghani/light_in_tissue
Light transport in soft tissue. Hamid Dehghani, Univ. Exeter, UK
| Name |
light_in_tissue |
| Group |
Dehghani |
| Matrix ID |
1873 |
|
Num Rows
|
29,282 |
|
Num Cols
|
29,282 |
|
Nonzeros
|
406,084 |
|
Pattern Entries
|
406,084 |
|
Kind
|
Electromagnetics Problem |
|
Symmetric
|
No |
|
Date
|
2007 |
|
Author
|
H. Dehghani |
|
Editor
|
T. Davis |
| Structural Rank |
29,282 |
| Structural Rank Full |
true |
|
Num Dmperm Blocks
|
1 |
|
Strongly Connect Components
|
1 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
100% |
|
Numeric Symmetry
|
0% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
complex |
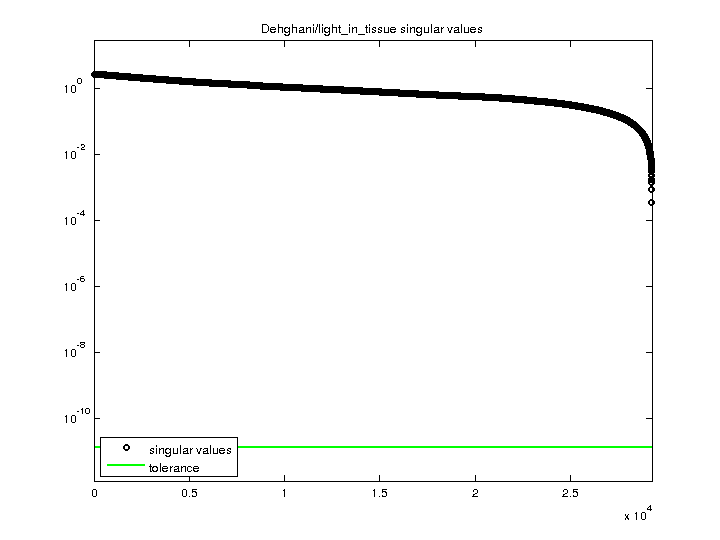
| SVD Statistics |
| Matrix Norm |
2.663552e+00 |
| Minimum Singular Value |
3.405251e-04 |
| Condition Number |
7.821896e+03
|
| Rank |
29,282 |
| sprank(A)-rank(A) |
0 |
| Null Space Dimension |
0 |
| Full Numerical Rank? |
yes |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
% The problem is solving the fluence (PHI) of light in soft tissue using
% a simplified 3rd spherical harmonic expansion (SPN3) of the Radiative
% Transport Equation. There are two coupled equations to solve:
% M1*phi1 = Q + (M2*phi2) eq(1)
% (M4 - (M3*inv(M1)*M2))*phi2 = -2/3*Q + M3*inv(M1)*Q eq(2)
% PHI = phi1 - (1/3).*phi2 eq(3)
Problem = UFget ('Dehghani/light_in_tissue') ;
A = Problem.A ; % get the problem
Q = Problem.aux.Q ;
k = size (A,1) / 2 ;
M1 = A (1:k,1:k) ;
M2 = A (1:k,k+1:end) ;
M3 = A (k+1:end, 1:k) ;
M4 = A (k+1:end, k+1:end) ;
elements = Problem.aux.elements ;
nodes = Problem.aux.nodes ;
Q2 = (-(2/3).*Q) + (M3*(M1\Q)) ; % create rhs for equation 2
Q2 = [sparse(k,1) ; Q2] ;
phi2 = A\Q2 ; % solve for phi2
phi2 = phi2 (end/2+1:end,:) ;
Q1 = Q + M2*phi2 ; % calculate rhs for equation 1
phi1 = M1\Q1; % solve for phi1
PHI = phi1 - (1/3).*phi2;
figure (1) ; clf % plot results
trisurf(elements, nodes(:,1), nodes(:,2), nodes(:,3), log(abs(PHI))) ;
shading interp ;
view (2) ;
colorbar('horiz') ;
axis equal ;
axis off ;
colormap hot ;
|