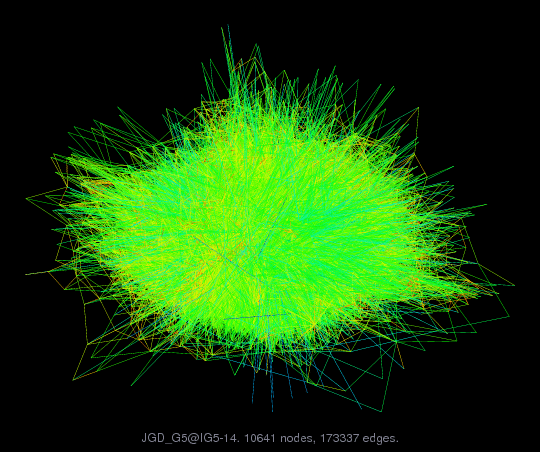
JGD_G5/IG5-14
Decomposable subspaces at degree d of the invariant ring of G5, Nicolas Thiery.
| Name |
IG5-14 |
| Group |
JGD_G5 |
| Matrix ID |
1973 |
|
Num Rows
|
6,735 |
|
Num Cols
|
7,621 |
|
Nonzeros
|
173,337 |
|
Pattern Entries
|
173,337 |
|
Kind
|
Combinatorial Problem |
|
Symmetric
|
No |
|
Date
|
2008 |
|
Author
|
N. Thiery |
|
Editor
|
J.-G. Dumas |
| Structural Rank |
3,906 |
| Structural Rank Full |
false |
|
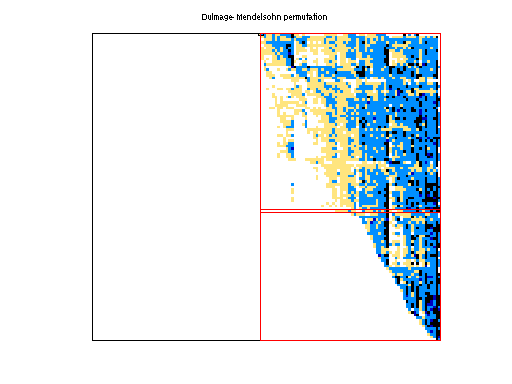
Num Dmperm Blocks
|
11 |
|
Strongly Connect Components
|
3,716 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
0% |
|
Numeric Symmetry
|
0% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
integer |
| SVD Statistics |
| Matrix Norm |
1.244258e+02 |
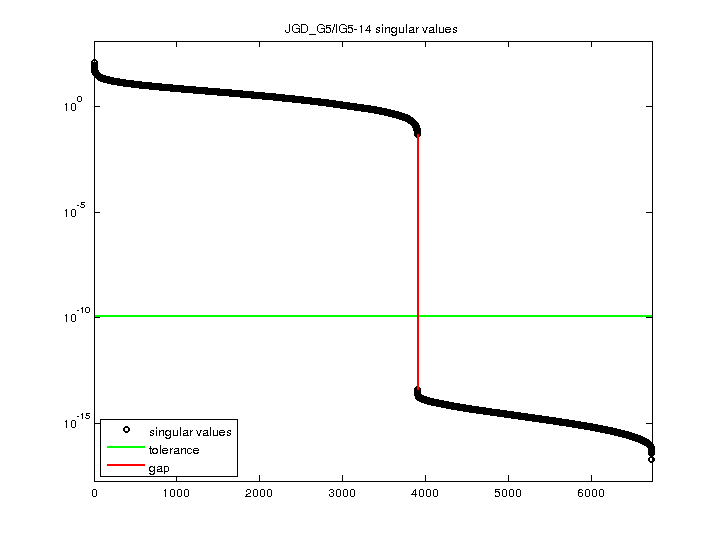
| Minimum Singular Value |
1.872302e-17 |
| Condition Number |
6.645604e+18
|
| Rank |
3,906 |
| sprank(A)-rank(A) |
0 |
| Null Space Dimension |
2,829 |
| Full Numerical Rank? |
no |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
Decomposable subspaces at degree d of the invariant ring of G5, Nicolas Thiery.
Univ. Paris Sud.
From Jean-Guillaume Dumas' Sparse Integer Matrix Collection,
http://ljk.imag.fr/membres/Jean-Guillaume.Dumas/simc.html
http://www.lapcs.univ-lyon1.fr/~nthiery/LinearAlgebra/
Linear Algebra for combinatorics
Abstract: Computations in algebraic combinatorics often boils down to
sparse linear algebra over some exact field. Such computations are
usually done in high level computer algebra systems like MuPAD or
Maple, which are reasonnably efficient when the ground field requires
symbolic computations. However, when the ground field is, say Q or
Z/pZ, the use of external specialized libraries becomes necessary. This
document, geared toward developpers of such libraries, present a brief
overview of my needs, which seems to be fairly typical in the
community.
IG5-6: 30 x 77 : rang = 30 (Iteratif: 0.01 s, Gauss: 0.01 s)
IG5-7: 62 x 150 : rang = 62 (Iteratif: 0.02 s, Gauss: 0.01 s)
IG5-8: 156 x 292 : rang = 154 (Iteratif: 0.08 s, Gauss: 0.01 s)
IG5-9: 342 x 540 : rang = 308 (Iteratif: 0.46 s, Gauss: 0.02 s)
IG5-10: 652 x 976 : rang = 527 (Iteratif: 2.1 s, Gauss: 0.07 s)
IG5-11: 1227 x 1692 : rang = 902 (Iteratif: 7.5 s, Gauss: 0.22 s)
IG5-12: 2296 x 2875 : rang = 1578 (Iteratif: 26 s, Gauss: 0.93 s)
IG5-13: 3994 x 4731 : rang = 2532 (Iteratif: 80 s, Gauss: 3.35 s)
IG5-14: 6727 x 7621 : rang = 3906 (Iteratif: 244 s, Gauss: 10.06 s)
IG5-15: 11358 x 11987 : rang = 6146 (Iteratif: s, Gauss: 29.74 s)
IG5-16: 18485 x 18829 : rang = 9519 (Iteratif: s, Gauss: 621.97 s)
IG5-17: 27944 x 30131 : rang = 14060 (Iteratif: s, Gauss: 1973.8 s)
Filename in JGD collection: G5/IG5-14.txt2
|