Newman/netscience
co-authoship of scientists in network theory & experiments
| Name |
netscience |
| Group |
Newman |
| Matrix ID |
2401 |
|
Num Rows
|
1,589 |
|
Num Cols
|
1,589 |
|
Nonzeros
|
5,484 |
|
Pattern Entries
|
5,484 |
|
Kind
|
Undirected Weighted Graph |
|
Symmetric
|
Yes |
|
Date
|
2006 |
|
Author
|
M. Newman |
|
Editor
|
M. Newman |
| Structural Rank |
|
| Structural Rank Full |
|
|
Num Dmperm Blocks
|
|
|
Strongly Connect Components
|
396 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
100% |
|
Numeric Symmetry
|
100% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
real |
| SVD Statistics |
| Matrix Norm |
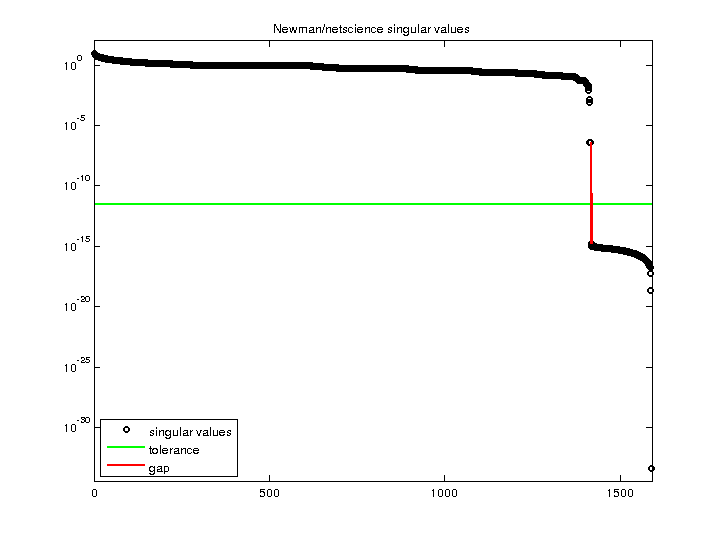
9.728574e+00 |
| Minimum Singular Value |
0 |
| Condition Number |
Inf
|
| Rank |
1,416 |
| sprank(A)-rank(A) |
|
| Null Space Dimension |
173 |
| Full Numerical Rank? |
no |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
Network collection from M. Newman
http://www-personal.umich.edu/~mejn/netdata/
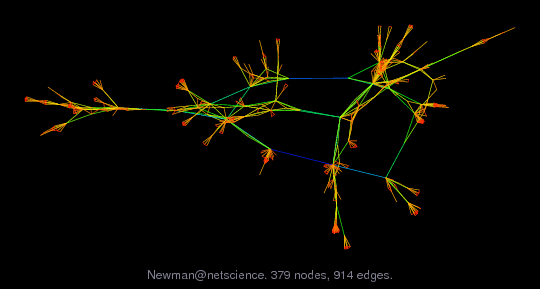
The graph netscience contains a coauthorship network of scientists
working on network theory and experiment, as compiled by M. Newman in May
2006. The network was compiled from the bibliographies of two review
articles on networks, M. E. J. Newman, SIAM Review 45, 167-256 (2003) and
S. Boccaletti et al., Physics Reports 424, 175-308 (2006), with a few
additional references added by hand. The version given here contains all
components of the network, for a total of 1589 scientists, and not just the
largest component of 379 scientists previously published. The network is
weighted, with weights assigned as described in M. E. J. Newman,
Phys. Rev. E 64, 016132 (2001).
If you make use of these data, please cite M. E. J. Newman, Finding
community structure in networks using the eigenvectors of matrices,
Preprint physics/0605087 (2006).
|