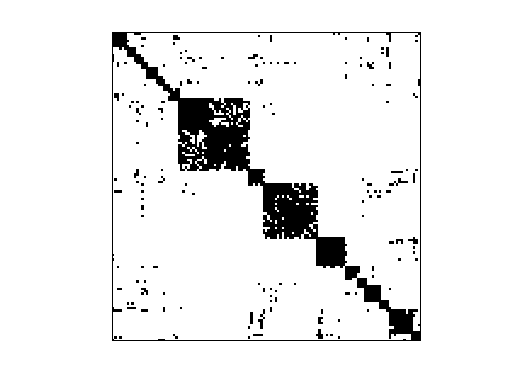
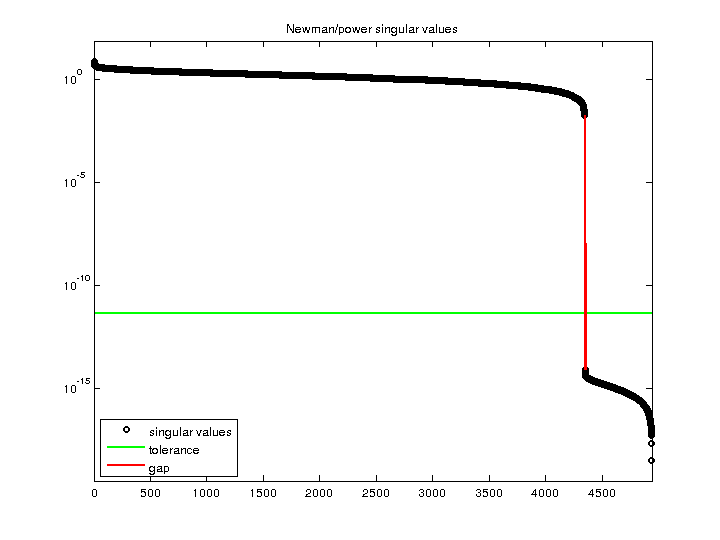
Newman/power
Western States Power Grid, Watts & Strogatz
| Name |
power |
| Group |
Newman |
| Matrix ID |
2404 |
|
Num Rows
|
4,941 |
|
Num Cols
|
4,941 |
|
Nonzeros
|
13,188 |
|
Pattern Entries
|
13,188 |
|
Kind
|
Undirected Graph |
|
Symmetric
|
Yes |
|
Date
|
1998 |
|
Author
|
D. Watts, S. Strogatz |
|
Editor
|
M. Newman |
| Structural Rank |
|
| Structural Rank Full |
|
|
Num Dmperm Blocks
|
|
|
Strongly Connect Components
|
1 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
100% |
|
Numeric Symmetry
|
100% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
binary |
| SVD Statistics |
| Matrix Norm |
7.483051e+00 |
| Minimum Singular Value |
3.108519e-19 |
| Condition Number |
2.407272e+19
|
| Rank |
4,348 |
| sprank(A)-rank(A) |
|
| Null Space Dimension |
593 |
| Full Numerical Rank? |
no |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
Network collection from M. Newman
http://www-personal.umich.edu/~mejn/netdata/
Western States Power Grid
Compiled by Duncan Watts and Steven Strogatz
The graph "power" contains an undirected unweighted representation of the
topology of the Western States Power Grid of the United States, compiled by
Duncan Watts and Steven Strogatz. The data are from the web site of
Prof. Duncan Watts at Columbia University,
http://cdg.columbia.edu/cdg/datasets. Node IDs are the same as those used
by Prof. Watts.
These data can be cited as:
D. J. Watts and S. H. Strogatz, "Collective dynamics of `small-world
networks", Nature 393, 440-442 (1998).
Note by Tim Davis: this graph has the same number of nodes and edges
as the Pajek/USpowerGrid graph. They are related as follows:
Prob1 = UFget ('Newman/power')
Prob2 = UFget ('Pajek/USpowerGrid')
A = Prob1.A ;
B = Prob2.B ;
n = size (A,1) ;
p = [2:n 1] ;
isequal (A (p,p), B)
This is because of the way the Pajek data set converted 0-based node IDs
to 1-based. In the Pajek set, node 0 is renamed node n, and this
translation was then imported into the Pajek/ Group in the UF collection.
The standard convention in MATLAB, and (elsewhere) in the UF Collection,
is to map nodes 0:n-1 of a zero-based graph to 1:n. The latter translation
preserves the relative numbering of all the nodes; the Pajek translation
does not.
Although technically Newman/power is a duplicate matrix, I have added it
to the UF Collection to preserve the original relative node ordering.
|