Priebel/176bit
Quadratic sieve; factoring a 176bit number. D. Priebel, Tenn. Tech Univ
| Name |
176bit |
| Group |
Priebel |
| Matrix ID |
2253 |
|
Num Rows
|
7,441 |
|
Num Cols
|
7,431 |
|
Nonzeros
|
82,270 |
|
Pattern Entries
|
82,270 |
|
Kind
|
Combinatorial Problem |
|
Symmetric
|
No |
|
Date
|
2009 |
|
Author
|
D. Priebel |
|
Editor
|
T. Davis |
| Structural Rank |
7,110 |
| Structural Rank Full |
false |
|
Num Dmperm Blocks
|
893 |
|
Strongly Connect Components
|
282 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
0% |
|
Numeric Symmetry
|
0% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
binary |
| SVD Statistics |
| Matrix Norm |
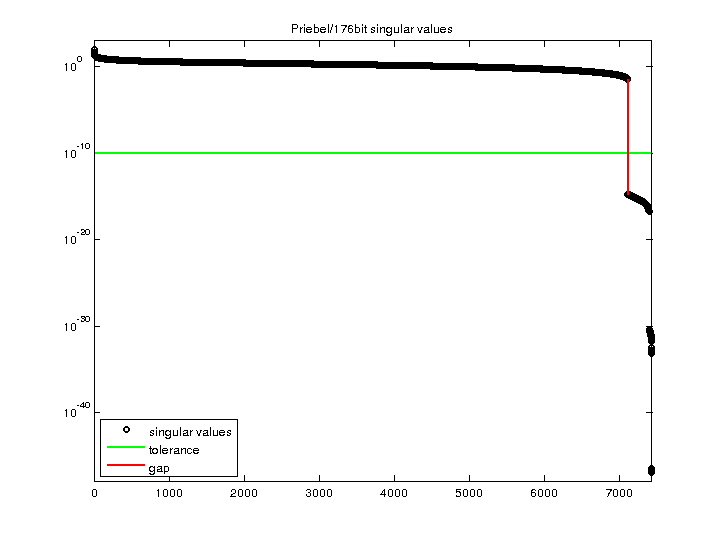
9.619242e+01 |
| Minimum Singular Value |
1.319478e-47 |
| Condition Number |
7.290185e+48
|
| Rank |
7,110 |
| sprank(A)-rank(A) |
0 |
| Null Space Dimension |
321 |
| Full Numerical Rank? |
no |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
Each column in the matrix corresponds to a number in the factor base
less than some bound B. Each row corresponds to a smooth number (able
to be completely factored over the factor base). Each value in a row
binary vector corresponds to the exponent of the factor base mod 2.
For example:
factor base: 2 7 23
smooth numbers: 46, 28, 322
2^1 * 23^1 = 46
2^2 * 7^1 = 28
2^1 * 7^1 * 23^1 = 322
Matrix:
101
010
111
A solution to the matrix is considered to be a set of rows which when
combined in GF2 produce a null vector. Thus, if you multiply each of
the smooth numbers which correspond to that particular set of rows you
will get a number with only even exponents, making it a perfect
square. In the above example you can see that combining the 3 vectors
results in a null vector and, indeed, it is a perfect square: 644^2.
Problem.A: A GF(2) matrix constructed from the exponents of the
factorization of the smooth numbers over the factor base. A solution of
this matrix is a kernel (nullspace). Such a solution has a 1/2 chance of
being a factorization of N.
Problem.aux.factor_base: The factor base used. factor_base(j) corresponds
to column j of the matrix. Note that a given column may or may not have
nonzero elements in the matrix.
Problem.aux.smooth_number: The smooth numbers, smooth over the factor
base. smooth_number(i) corresponds to row i of the matrix.
Problem.aux.solution: A sample solution to the matrix. Combine, in GF(2)
the rows with these indicies to produce a solution to the matrix with the
additional property that it factors N (a matrix solution only has 1/2
probability of factoring N).
Problem specific information:
n = 73363722971930954428433124842779099222294372095286387 (176-bits)
passes primality test, n is composite, continuing...
1) Initial bound: 180000, pi(180000) estimate: 14875,
largest found: 162359 (actual bound)
2) Number of quadratic residues estimate: 9918, actual number found: 7431
3) Modular square roots found: 14862(2x residues)
4) Constructing smooth number list [sieving] (can take a while)...
Sieving for: 7441
5. Constructing a matrix of size: 7441x7432
Set a total of 82270 exponents, with 3725 negatives
Matrix solution found with: 2983 combinations
Divisor: 236037985789994529800050193 (probably prime)
Divisor: 310813205452462332837525059 (probably prime)
|