Quaglino/viscoplastic1
FEM discretization of a viscoplastic collision problem, Alessio Quaglino
| Name |
viscoplastic1 |
| Group |
Quaglino |
| Matrix ID |
1868 |
|
Num Rows
|
4,326 |
|
Num Cols
|
4,326 |
|
Nonzeros
|
61,166 |
|
Pattern Entries
|
61,166 |
|
Kind
|
Materials Problem |
|
Symmetric
|
No |
|
Date
|
2007 |
|
Author
|
A. Quaglino |
|
Editor
|
T. Davis |
| Structural Rank |
4,326 |
| Structural Rank Full |
true |
|
Num Dmperm Blocks
|
1 |
|
Strongly Connect Components
|
1 |
|
Num Explicit Zeros
|
0 |
|
Pattern Symmetry
|
74.1% |
|
Numeric Symmetry
|
0% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
real |
| SVD Statistics |
| Matrix Norm |
7.387435e+01 |
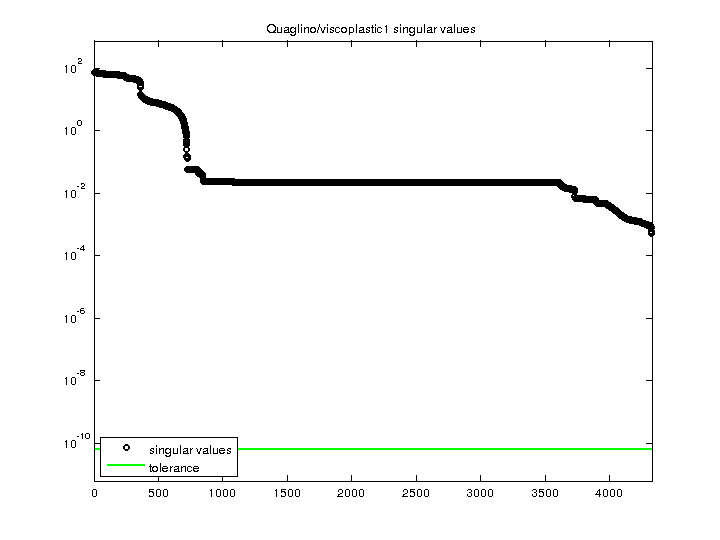
| Minimum Singular Value |
5.290540e-04 |
| Condition Number |
1.396348e+05
|
| Rank |
4,326 |
| sprank(A)-rank(A) |
0 |
| Null Space Dimension |
0 |
| Full Numerical Rank? |
yes |
| Download Singular Values |
MATLAB
|
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
The matrix is in the form [A11 A12 ; A21 A22] where A11 and A22 are diagonal.
Originally, the matrices in this set were poorly scaled, but this was resolved
by a scale factor of the form [A11 A12*e ; A21/e A4] where the scalar e is
of magnitude 1e2 but can be 1e6 or 1e7 for a stiff material. The Problem.A
matrix is the properly scaled problem. The Problem.aux.C{1:7} matrices have
been "unscaled" with a factor e = 10.^(-(1:7)), to give a sequence of matrices
that are well scaled to poorly scaled, and thus well conditioned (C{1}) to
poorly conditioned (C{7}). This mimics the original poorly scaled and ill-
conditioned problem, and may be of interest for those developing algorithms
for automatic scaling. From a FEM discretization of a viscoplastic collision
problem, Alessio Quaglino.
|