Watson/Baumann
chemical master eqn, aij*h = prob of i->j transition in time h (Markov model)
| Name |
Baumann |
| Group |
Watson |
| Matrix ID |
1855 |
|
Num Rows
|
112,211 |
|
Num Cols
|
112,211 |
|
Nonzeros
|
748,331 |
|
Pattern Entries
|
760,631 |
|
Kind
|
2D/3D Problem |
|
Symmetric
|
No |
|
Date
|
2007 |
|
Author
|
L. Watson and J. Zhang |
|
Editor
|
T. Davis |
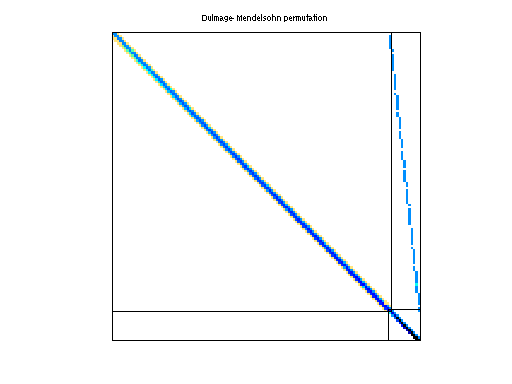
| Structural Rank |
112,211 |
| Structural Rank Full |
true |
|
Num Dmperm Blocks
|
2 |
|
Strongly Connect Components
|
2 |
|
Num Explicit Zeros
|
12,300 |
|
Pattern Symmetry
|
100% |
|
Numeric Symmetry
|
0% |
|
Cholesky Candidate
|
no |
|
Positive Definite
|
no |
|
Type
|
real |
| Download |
MATLAB
Rutherford Boeing
Matrix Market
|
| Notes |
The ODE system \frac{dp}{dt}=Qp is what we call a chemical master equation (a
Kolmogorov's backward/forward equation). Q is a sparse asymmetric matrix,
whose off-diagonal entries are non-negative and row sum to zero. On each row,
q_{ij}h gives the probability the system makes a transition from current state
i to some other state j, in small time interval h. By "state", we mean a
possible combination of number of molecules in each chemical species. Now, h
is small enough so that only one reaction happens. In this way q_{ij} is
nonzero only if there exists a chemical reaction that connects state i and j,
i.e. j=i+s_k, s_k's are constant state vectors that correspond to every
reaction. Say we have M reactions, then there are at most M+1 nonzero
entries on each row of Q. On the other hand, the number of possible
combination of molecules is huge, which means the dimension of Q is huge.
The linear system we want to solve is (I - Q/lambda)x=b, and we have
to solve it several times. (Here lambda is a constant). Problem.A is the Q
matrix. This is a medium test problem; the largest has dimension 10^8.
It has the nonzero pattern of a 11-by-101-by-101 mesh.
|